С другой стороны, этот же дифференциал можно расписать какПаракомплексные числа.
Алгебраические свойства.
Рассмотрим числа вида
a+jb где a,b - действительные числа, j2=1. Такие числа Каратаев называет паракомплексными (http://karataev.hotmail.ru) Они по определению образуют 2D векторное пространство над полем R , а значит, абелеву аддитивную группу. Определим их умножение обычным образом; непосредственно можно проверить коммутативность, ассоциативность и дистрибутивность этой операции. Однако эти числа не образуют поле, в их множестве есть делители нуля.Докажем это. Рассмотрим многочлен
x^2-1. На основании указанных свойств умножения его можно разложить на множители (x+1)(x-1), этим множителям соответствуют корни -1 и 1. Однако по построению существует ещё 1 корень, а именно j. Отсюда видно, что j+1, j-1 и есть искомые делители нуля.Мера Лебега и топология.
Мера Лебега определяется на множестве паракомплексных чисел обычным образом, через овеществление, т.е. как на обычной плоскости. Аналогично можно упорядочить, см.
http://fit-rulez.narod.ru/research/linorderfeatru.htm Вводится топология покоординатной сходимости.Функция паракомплексной переменной.
Топология позволяет определить непрерывность отображения. Можно определить также дифференцируемость, есть аналоги уравнений Коши-Римана. Сначала определим формальные производные: Рассмотрим дифференцируемую функцию паракомплексной переменной, принимающую паракомплексные значения.
f(x)=u(a,b)+jv(a,b), где x=a+jb Распишем дифференциал этой функции:С другой стороны, этот же дифференциал можно расписать как
Приравнивая полученные выражения покомпонентно, имеем
u'=¶ u/¶ a=¶ v/¶ b,
v'=¶ u/¶ b=¶ v¶ a.
Эти уравнения являются аналогами уравнений Коши-Римана, они необходимы для дифференцируемости функции.
Отсюда получим гармоническое уравнение для аналитической функции
¶ 2f/¶ a2-¶ 2f/¶ b2=0. Решив это уравнение гиперболического (а не эллиптического) типа, получим явный вид гармонической или аналитической функции
Из уравнений выводится аналог теоремы Коши: интеграл любой дифференцируемой функции по замкнутому контуру внутри односвязной области равен нулю. Доказательство следует из формулы Грина.
Мы можем рассмотреть ряды и разложение в ряд для функции паракомплексной переменной (поскольку топология определена). Разлагая в ряд Тейлора функции
exp,sin,cos, получаем аналог формулы Эйлера: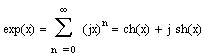
Функция нескольких паракомплексных переменных.
Применим последнюю формулу к функции нескольких паракомплексных переменных. Имеем:
f(x1+jy1,x2+jy2,…,xn+jyn)=f1(x1+y1,x2+jy2,…,xn+jyn)+f2(x1-y1,x2+jy2,…,xn+jyn)=å f(x1± y1,x2± y2,…,xn± yn), т.е. дифференцируемая функция n паракомплексных переменных в самом деле является комбинацией дифференцируемых функций n вещественных переменных.