Linear Order Features

This paper is dedicated for exploring linear order especially in finite dimensional vector spaces including complex. Note that scalar product is not required i. e. the space is not necessarily unitary.

Even though it is known as common lexicographic order for Boolean vectors, the topic is not developed rather well for more complicated real and complex numbers as well as their vector spaces.

Let L be an n dimensional arithmetic space upon linearly ordered field P. For any other vector space we can use an isomorphism.

Let's introduce a < relation using the algorithm below and let's prove that it is linear order. We'll use Latin letters for vectors and indexes for coordinates.

So if a<b it is not possible that b<a; thus this relation is anti symmetric.

Now let a<b and b<c, a differs from b by k^th coordinate as well as b differs from c by l^th coordinate. The 3 possible cases are described below:

1. k=l
2. k<l
3. k>l

In the first case, a_k<b_k<c_k, so a<c. In the second case, a_k=b_k<c_k, so a<c. In the third case, a_l<b_l=c_l, so a<c. Thus the relation is transitive. So it is an order. For any pair of a,b one and only one statement takes place: a=b, a<b, or b<a i.e. the order is linear.

Let us analyze real valued finite dimensional space. Because the field of real numbers is linearly ordered, the space is also linearly ordered by means of the algorithm. This is still applicable to the field of complex numbers since it forms vector space upon the field of real numbers. Now we can order any complex valued finite dimensional vector space.

We often find a statement that complex numbers field cannot be ordered linearly. This really means no good order. We say an order is good if it satisfies some additional axioms; for complex numbers that does not exist. Let us prove it.

Suppose that's not true. So it's possible to compare any 2 complex numbers, for instance i and 0. If i>0 we multiply the inequality to i and get -1>0. Otherwise, i<0 we multiply the inequality to negative number i, change its sign, and get тАУ1>0.

The space is completely ordered if and only if the field is ordered completely.

If there is a system of vectors i.e. a nonempty subset of the vector space, let us examine the set of the first components of vectors of that system. The set is not empty by definition. If it consists of one element, the corresponding vector is the exact lower bound; if not, examine the subset of corresponding vectors with the second components, and so on.

Let V={v₁; v₂; тАж} be a subset of the field. The exact lower bound of V'={( v₁,0,тАж,0); (v₂,0,тАж,0);тАж} is always (inf V,0,тАж,0); in other words, the relation copies order from the field to the vector space. So if the field has a subset with no lower bound in it, there also exists a vector set with no lower bound in it.

As derived from the Archimedes axiom, the fields of real and complex numbers are not ordered completely.

The order depends on basis. It's recommended fixing a basis. Otherwise, we'll get a different order for each basis.

This algorithm cannot be applied to infinite dimensional vector spaces.

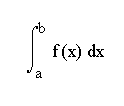
However it is not usual curve integral, it is not obviously suitable for common functions. It is possible to define an improper integral.

Another possible application is measure theory. The question is, if there is a distance, what kind of set it could be measured with? We know, the measuring set is ordered and has an addition operation with several properties.